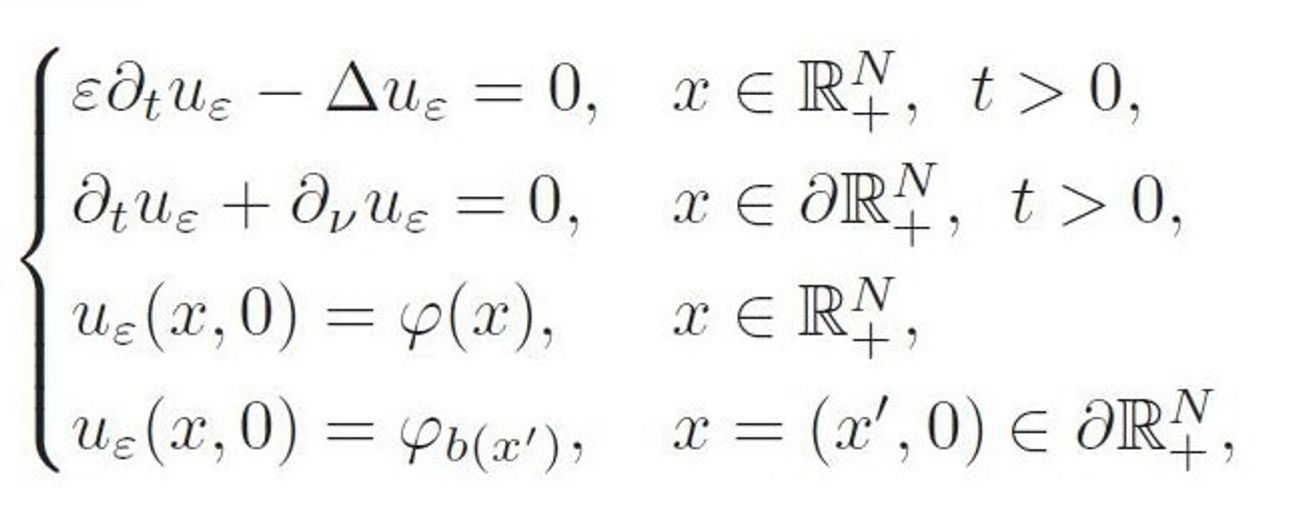数理・情報科学課程の川上竜樹教授が受賞題目「楕円型・放物型方程式と動的境界条件の漸近解析」にて第12回函数方程式論分科会福原賞を受賞しました。
この賞は、日本数学会 函数方程式論分科会において主な研究活動を行っている研究者の中で, 函数方程式論分科会での特別講演あるいは研究集会「微分方程式の総合的研究」で招待講演を行った方々のうち, 優れた業績を上げた方を中心に顕彰を行うものです。
川上教授は、これまで非線形放物型方程式の解構造及び漸近挙動を中心に研究を行なってきていますが、受賞理由としてはComenius大学教授のMarek Fila氏と東京大学教授の石毛和弘氏と共同で行った領域の境界上での時間発展を考慮した動的境界条件付き楕円型方程式及び放物型方程式の一連の研究が挙げられます。
これにより、動的境界条件付き非線形楕円型方程式の時間局所解、時間大域解、定常解の存在が全て同値であるという顕著な解構造を発見しました。さらに動的境界条件下の熱方程式の拡散極限が同条件下のラプラス方程式の自然な解を選択することを導きました。また、石毛氏と共同で開発した放物型方程式に対する解の高次漸近展開理論を、最近研究が盛んな非局所拡散現象のモデル方程式である分数冪放物型方程式を範疇に含める形に再構築した研究も受賞理由に挙げられています。
2020年度(第12回) 函数方程式論 福原賞 賞状
序論で考察されている数式
【式の解説】
はN次元半空間(簡単な例で言えば, 2次元の-平面の の部分)
はその境界(上の例で言えば, 直線 , つまり 軸)です。
一本目の式が熱拡散方程式, 2本目の式が動的境界条件です。