「素数定理」 原奨馬

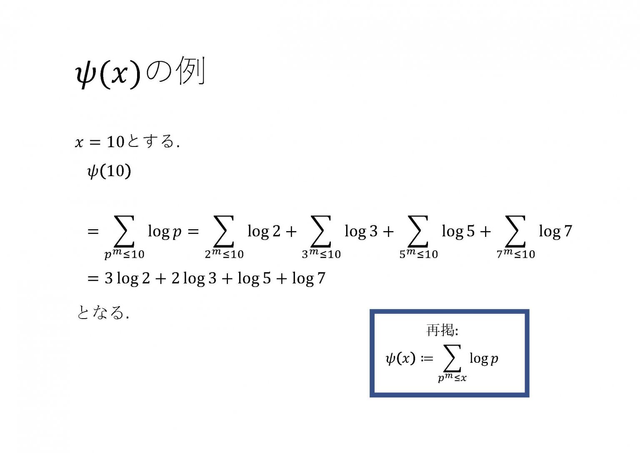
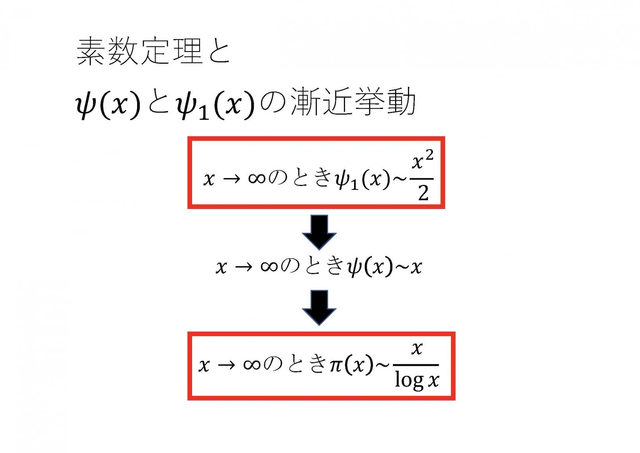
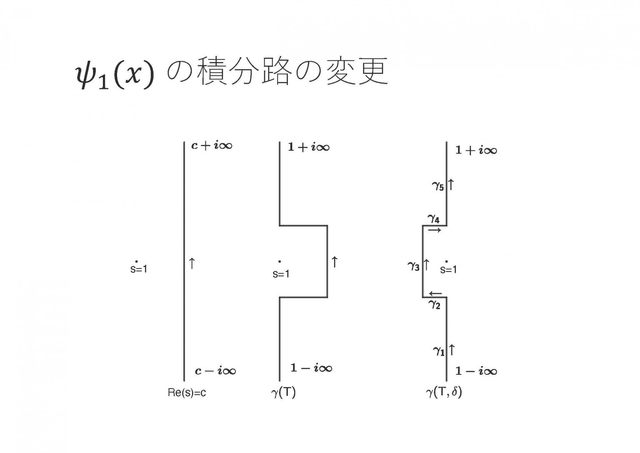
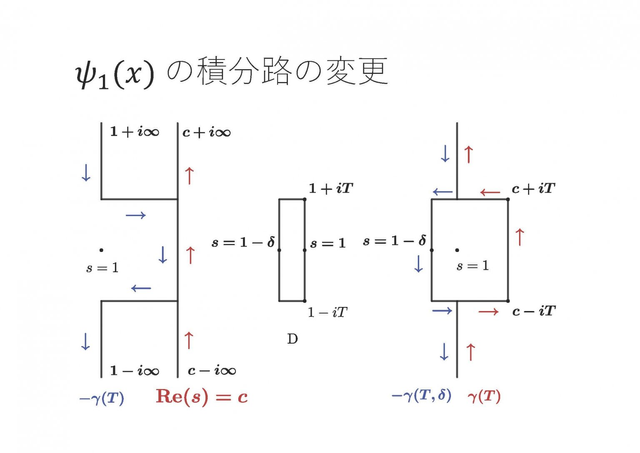
素数は未知の部分が多く、メルセンヌ素数や双子素数などのように、素数の中での分類はされているが、素数全体の分布は未だに知られていない。そこで本研究では素数の分布に関して重要な役割を果たす素数定理に関して、その証明を理解することを目標とした。素数定理とは、ある正の実数 x 以下の素数のコスを数える素数計測関数 π(x) の漸近挙動を述べたものである。この素数定理の証明にはいつくかの方法が知られているが、本論文においては ζ 関数や解析接続、複素積分の性質を用いた複素解析的な手法を採用した。この ζ 関数は完全に解析された関数ではないが、素数との関わりが深いことが知られており、証明においてもこの関数の性質の解析が重要な役割を果たしている。